«مسائل جایزه هزاره» در واقع ۷ قضیه دشوار ریاضیات می باشند که سال ۲۰۰۰ «مؤسسه ریاضیات کِلی» آنها را تعیین کرده‌اند. این مؤسسه برای حل یا اثبات هر قضیه یک‌میلیون دلار جایزه در نظر گرفته است. تا بحال یکی از این مسائل حل‌نشدنی، با گفتن «گمان پوانکاره» به جواب رسیده اما تا به‌ امروز ۶ قضیه دیگر هم چنان حل‌نشده باقی مانده‌اند. در این نوشته از دیجیاتو، تصمیم داریم مسائل هزاره را مرور کنیم و آنها را با زبانی ساده توضیح دهیم.

تاریخچه مسائل هزاره

اولین بار ۲۴ مه ۲۰۰۰، به‌منظور بزرگداشت ریاضیات در اغاز هزاره تازه، مؤسسه ریاضیات کِلی (CMI) در کمبریج، ماساچوست، ۷ قضیه‌ جایزه‌دار را تعیین کرد. این جوایز به‌منظور ثبت برخی از دشوارترین مسائلی که ریاضی‌دانان در اغاز هزاره دوم با آنها دچار بودند، طراحی شد.

این ۷ قضیه انتخاب شدند. درنهایت، هیئت‌مدیره CMI جایزه یک‌میلیون دلاری را برای هرکدام از ۷ قضیه (درمجموع ۷ میلیون دلار) تعریف کرد.

تمرکز این هیئت روی سؤالات کلاسیک مهمی است که سال‌ها بدون راه‌حل باقی مانده‌اند. مقصد این کار علاوه‌بر جلب دقت عموم به این حقیقت که در ریاضیات تا این مدت مرزهای ناشناخته و مسائل حل‌نشده مهمی وجود دارد، پافشاری بر اهمیت تلاش برای حل عمیق‌ترین و دشوارترین مسائل و تقدیر از دستاوردهایی مهم در تاریخ ریاضیات است.

۷ قضیه‌ با گفتن مسائل جایزه هزاره یا مسائل حل‌نشدنی نقل شدند، شامل موارد زیر بودند:

• گمان پوانکاره
• فرضیه ریمان
• قضیه P در روبه رو NP
• گمان بیرچ و سوینرتون-دایر
• گمان هاج
• معادله ناویر-استوکس
• نظریه یانگ-میلز

دلنشین این است که از این ۷ قضیه لاینحل ریاضی، قضیه «گمان پوانکاره» حل شده است اما ۶ قضیه دیگر هم چنان حل‌نشده باقی مانده‌اند. در ادامه، هریک از این مسائل را توضیح می‌دهیم.

گمان پوانکاره؛ قضیه حل‌شده

گمان پوانکاره یکی از سؤالات مشهور در ریاضیات است که سال ۱۹۰۴ ریاضی‌دان فرانسوی، «هانری پوانکاره»، نقل کرد. برای فهمیدن گمان پوانکاره ابتدا باید مفهوم «اتصال ساده» را بازدید کنیم. درصورتی که هر حلقه‌ای را که روی فضایی سبه‌بعدی رسم کنیم، بتوانیم بدون پاره‌کردن یا برداشتن از سطح در نقطه‌ای جمع کنیم، آن فضا فضای سه‌بعدی اتصال ساده دارد.

برای مثال، سطح یک دایره (کره دو‌بعدی) اتصال ساده دارد؛ چون هر حلقه‌ای که روی آن بکشیم، می‌توانیم آن را در نقطه‌ای جمع کنیم اما دونات این‌طور نیست؛ چون حلقه‌هایی را که دور سوراخ آن کشیده خواهد شد، نمی‌توان بدون پاره‌کردن، در یک نقطه جمع کرد.

پوانکاره می‌پرسد آیا این ویژگی اتصال ساده می‌تواند برای تعریف یکتایی منیفولدهای سه‌بعدی (فضای سه‌بعدی اقلیدسی) منفعت گیری شود؟ به گفتن ساده‌تر، آیا هر منیفولد سه‌بعدی که اتصال ساده دارد، کره‌ای سه‌بعدی است؟

حل قضیه گمان پوانکاره

بین سال‌های ۲۰۰۲ و ۲۰۰۳، «گریگوری پرلمان»، ریاضی‌دان روس، ۳ مقاله در اینترنت انتشار کرد که شامل اثباتی مختصر برای گمان پوانکاره می بود. اثبات پایه‌ای او را چندین ریاضی‌دان گسترش داده شد و تا ۲۰۰۶ به‌طور عمومی راه‌حلی معتبر شناخته شد.

پرلمان نشان داد هر منیفولد سه‌بعدی با منفعت گیری از مجموعه‌ای از قطعات استاندارد با یکی از ۸ هندسه ممکن ساخته می‌شود. (این ۸ نوع هندسه شامل ساختارهای خاصی همانند فضاهای کروی، هذلولی، اقلیدسی و هندسه‌های دیگر است که هرکدام خصوصیات ریاضی متغیری دارند.) به گفتن ساده‌تر، هر فضای سه‌بعدی پیچیده را می‌توان به قطعاتی ساده‌تر و با ساختارهای اشکار تقسیم کرد.

راه‌حل پرلمان یکی از دستاوردهای بزرگ ریاضیاتی قرن بیستم شناخته می‌شود. سال ۲۰۰۶، مدال فیلدز به‌خاطر این دستاورد به او اعطا شد که یقیناً آن را نپذیرفت. این چنین سال ۲۰۱۰، CMI جایزه قضیه هزاره را برای اثبات گمان پوانکاره به پرلمان نظر داد اما او این جایزه را نیز نپذیرفت.

فرضیه ریمان، در بین مسائل غیرقابل حل ریاضی

فرضیه ریمان را «گئورگ فردریش برنهارد ریمان»، ریاضیدان آلمانی، سال ۱۸۵۹ نقل کرد. این فرضیه به چگونگی توزیع اعداد اول در مجموعه اعداد طبیعی مرتبط است. اعداد اول اعدادی می باشند که فقط بر یک و خودشان قسمت‌پذیرند و باوجود نقش مهمشان، نظم خاصی در پراکندگی‌شان وجود ندارد.

ریمان دریافت توزیع اعداد اول می‌تواند به تابعی ریاضی به نام «تابع زتای ریمان» مرتبط باشد. تابع زتای ریمان به‌صورت زیر تعریف می‌شود که در آن s عددی مختلط است. این تابع برای مقادیر مختلفی از s مقدار می‌گیرد و وقتی که این مقدار به صفر برسد، ریشه‌ای برای تابع به‌ دست می‌آید.

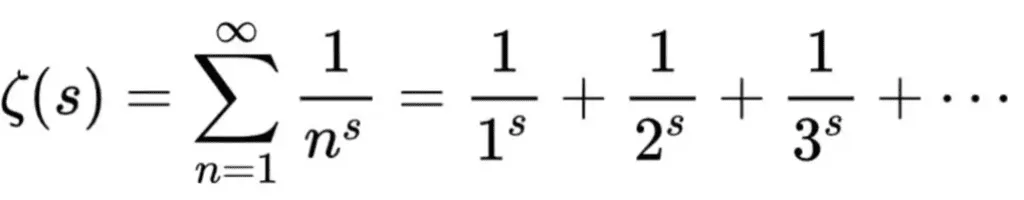
فرضیه ریمان گفتن می‌کند همه ریشه‌های معادله 𝜁(s)=0 روی خط عمودی خاصی به نام «خط بحرانی» قرار می‌گیرند.

این قضیه برای ۱۰ تریلیون ریشه اول بازدید شده و درست بوده است اما اثبات این که این فرضیه برای همه ریشه‌های معادله صحیح است، می‌تواند پرده از تعداد بسیاری از اسرار حوالی پراکندگی اعداد اول بردارد.

این گمان در زمان ریمان اثبات نشد و تا امروز هم اثبات یا رد قطعی آن ممکن نشده اما به‌گفتن یکی از مسائل بنیادین در نظریه اعداد باقی مانده است.

قضیه P در روبه رو NP

سوال P در روبه رو NP یکی از بزرگ‌ترین مسائل حل‌نشده در علوم رایانه و ریاضیات است که «استیون کوک» و «لئونید لوین»، سال ۱۹۷۱ به‌طور جدا گانه نقل کردند. این قضیه می‌پرسد آیا مسائلی که پاسخشان به‌راحتی قابل‌قبول است، به همان راحتی قابل‌حل هم می باشند یا خیر.

فکر کنید قضیه‌ای دارید که اگر فردی راه‌حلی برای آن بیاورد، شما می‌توانید به‌شدت بازدید کنید که راه‌حل درست است یا خیر اما امکان پذیر پیداکردن خودِ این راه‌حل به‌شکلی باورنکردنی دشوار باشد. اینجاست که دسته‌بندی‌های P و NP نقل خواهد شد:

• مسائل P شامل مسائلی می باشند که هم حل‌کردن هم بازدید جواب آنها آسان و سریع است (در وقتی معقول با پشتیبانی یک الگوریتم قابل‌حل می باشند).
• مسائل NP مسائلی می باشند که بازدید درستی جوابشان آسان است اما پیداکردن راه‌حل امکان پذیر دشوار باشد و زمان بسیاری بگیرد.

مثالی از مسائل NP قضیه «مسیر همیلتونی» است که در آن باید مسیر بازدید از برخی مکان‌ها را بدون تکرار اشکار کنیم. فکر کنید فردی مسیر را اشکار کرده و به شما داده است؛ می‌توانید به‌شدت بازدید کنید مسیر درست است یا خیر اما اگر خودتان بخواهید این چنین مسیری را از ابتدا اشکار کنید، به‌ گمان‌ زیاد با سختی بسیاری مواجه خواهید شد؛ چون تعداد ترکیب‌های ممکن زیاد زیاد است.

یکی دیگر از مثال‌های پیچیده قضیه اسکان دانشجویان در خوابگاه است. فکر کنید ۴۰۰ دانشجو داریم ولی فقط برای ۱۰۰ نفر جا دارید. این چنین رئیس دانشکده فهرستی از دانشجویان ناسازگار اراعه داده که نباید در انتخاب نهایی شما قرار بگیرند. اگر فردی لیستی به شما بدهد، می‌توانید سریع بازدید کنید شرایط رئیس را مراعات کرده‌اید یا خیر اما پیداکردن این لیست از ابتدا به‌علت تعداد زیاد ترکیب‌های ممکن زیاد سخت و زمان‌بر است.

سوال مهم این است که آیا این سختی به این معناست که واقعاً هیچ راه ساده‌ای برای حل این مسائل وجود ندارد یا فقط به این علت است که ما تا این مدت راه بهتری اشکار نکرده‌ایم؟ تا بحال هیچ‌کس نتوانسته ثابت کند مسائل NP واقعاً این‌قدر دشوار می باشند که هیچ راه مؤثری برای حل آنها وجود نداشته باشد.

اگر روزی ثابت شود P = NP یعنی همه مسائلی که راه‌حلشان به‌راحتی قابل‌بازدید است، در اصل قابل‌حل هم می باشند، این یافته تأثیرات بزرگی بر علوم رایانه، رمزنگاری و تعداد بسیاری از عرصه‌های دیگر خواهد داشت.

گمان برچ و سوینرتون-دایر

گمان برچ و سوینرتون-دایر را ریاضی‌دانان «برایان برچ» و «پیتر سوینرتون-دایر» در دهه ۱۹۶۰ نقل شد. این گمان یکی از با اهمیت ترین مسائل ریاضی است که رابطه هندسه و حرکت مجموعه‌ای از نقاط خاص، «نقاط گویا»، را روی خم‌های بیضوی بازدید می‌کند.

ریاضی‌دانان مدام به قضیه یافتن همه جواب‌های عدد صحیح برای معادلات جبری علاقه‌مند بوده‌اند. اقلیدس راه‌حل کاملی برای معادلات ساده اراعه داد اما این کار برای معادلات پیچیده‌تر زیاد دشوار می‌شود. سال ۱۹۷۰، «یو. و. ماتیاسویچ» نشان داد هیچ روش کلی وجود ندارد که بتوان با منفعت گیری از آن تعیین کرد معادلات جبری به‌طورکلی جواب صحیح دارند یا نه.

در موارد خاص می‌توان این قضیه را دقیق‌تر بازدید کرد. یکی از این موارد وقتی است که جواب‌های معادله نقاطی از تنوعی آبلی (نوعی خاص از ساختار جبری) باشند. دراین‌صورت، گمان برچ و سوینرتون-دایر گفتن می‌کند تعداد نقاط گویا روی خم بیضوی، به حرکت تابع ریاضی به نام «تابع زتا» در نزدیکی نقطه‌ای خاص، s=1، بستگی دارد.

به‌طور دقیق، این گمان می‌گوید اگر مقدار تابع زتا در s=1 برابر صفر باشد، تعداد نقاط گویا روی یک خم بیضوی بی‌نهایت است. در روبه رو، اگر مقدار تابع زتا در این نقطه صفر نباشد، تعداد نقاط گویا محدود خواهد می بود.

این گمان یکی از عمیق‌ترین ارتباطات بین هندسه و نظریه اعداد را برقرار می‌کند و اثبات آن می‌تواند به فهمیدن بهتری از خواص خم‌های بیضوی و کاربردهای عملی آنها، ازجمله در رمزنگاری، پشتیبانی کند.

گمان هاج: یکی دیگر از مسائل لاینحل ریاضی

گمان هاج را سال ۱۹۴۱ ریاضی‌دان اسکاتلندی، «ویلیام ولنتاین هاج»، نقل کرد. این قضیه به رابطه توپولوژی (شکل و ساختار کلی فضاها) و هندسه جبری می‌پردازد. این گمان می‌گوید در واریته‌های جبری تصویری (فضاهایی که با معادلات چندجمله‌ای تعریف خواهد شد)، می‌توان شکل کلی فضا را با ترکیب قطعات هندسی ساده‌تر به‌ دست آورد.

در قرن بیستم، ریاضی‌دانان به راه حلهای گسترش یافتهای برای بازدید شکل‌های پیچیده دست یافتند. ایده مهم این راه حلها این بوده است که ببینیم می‌توانیم شکلی پیچیده را با کنار هم گذاشتن بلوک‌های ساده و هندسی که هرکدام ابعاد مختلفی دارند، همانند‌سازی کنیم.

این تکنیک آن‌قدر مؤثر می بود که به‌مرور زمان در مسیرهای مختلفی گسترش اشکار کرد و درنهایت ابزارهای قدرتمندی پدید آورد که به ریاضی‌دانان پشتیبانی کرد مجموعه گسترده‌ای از شکل‌ها و فضاهای گوناگون را به‌صورت سیستماتیک دسته‌بندی کنند.

بااین‌حال، این گسترش و تعمیم‌ها علتشد مبنا هندسی این راه حلها در تعداد بسیاری از موارد مبهم شود. در برخی موارد حتی نیاز می بود تا قطعاتی اضافه شوند که معنی هندسی راحتی نداشتند و تنها به‌گفتن قسمت‌های اضافی برای تکمیل محاسبات منفعت گیری می‌شدند.

حال گمان هاج می‌گوید که برای واریته‌های خاصی، می‌توان برخی از ویژگی‌های توپولوژیکی فضا را فقط با منفعت گیری از قطعات هندسی قابل‌فهمیدن فرمود، آن‌ هم بدون نیاز به منفعت گیری از قطعاتی که معنی هندسی مشخصی ندارند. این قطعات هندسی قابل‌فهمیدن «سیکل‌های هاج» نام دارند. این گمان در ابعاد پایین‌تر (کمتر از ۴ بُعد) ثابت شده اما در ابعاد بالاتر تا این مدت ناشناخته باقی مانده و چالشی برای ریاضی‌دانان است.

معادله ناویر-استوکس

معادلات ناویر-استوکس را نیمه اول قرن ۱۹ ریاضی‌دانان و فیزیک‌دانان فرانسوی، «کلود-لویی ناویر» و «جرج استوکس»، به‌گفتن چارچوبی ریاضی برای توصیف حرکت سیالات نقل شد. به زبان ساده، این معادلات توضیح خواهند داد چطور نیروهای گوناگون همانند سختی و اصطکاک (چسبندگی) بر هر ذره از سیال تأثیر می‌گذارند و مقدار ویسکوزیته (گرانروی) سیال را تعیین می‌کنند. در واقع این معادلات گفتن دینامیکی از اعتدال نیروها در هر نقطه‌ای از سیال است.

وقتی که آب در رودخانه یا هوا در اتمسفر حرکت می‌کند، هنگامی با قایق در دریاچه حرکت می‌کنیم و امواجی در پشت قایق تشکیل خواهد شد یا هنگامی هواپیما با شدت بالا در آسمان پرواز می‌کند و جریان‌های آشفته و متلاطم هوا در پشت آن تشکیل می‌شود، همه انها مثال‌هایی از حرکت سیالات می باشند که نحوه حرکت و جریان ذراتشان با معادلات ناویر-استوکس توصیف می‌شود.

۲ سوال اساسی درمورد این معادلات تا این مدت بی جواب مانده است: آیا راه‌حل‌هایی برای این معادلات وجود دارد و اگر وجود دارد، آیا این راه‌حل‌ها یکتا می باشند؟ به‌عبارتدیگر، آیا می‌توانیم با قطعیت بگوییم سیالات همیشه به‌طور اشکار و قابل‌پیش‌بینی جریان می‌یابند؟ این قضیه اهمیت بسیاری دارد؛ چون اگر بتوانیم به آنها جواب بدهیم، می‌توانیم جریان‌های پیچیده سیالات را بهتر فهمیدن کرده، حتی اتفاق‌هایی همانند تلاطم یا آشفتگی هوا را پیش‌بینی کنیم.

این معادلات بیشتر از یک قرن پیش نوشته شده‌اند اما تا این مدت هم چالش‌های بسیاری برای فهمیدن و حل کامل آنها وجود دارد و ریاضی‌دانان و فیزیک‌دانان در کوششاند اسرار نهان در معادلات ناویر-استوکس را کشف کرده و بتوانند حرکت سیالات را دقیق‌تر پیش‌بینی کنند.

نظریه یانگ-میلز و «شکاف جرمی»

این نظریه را در دهه ۱۹۵۰ فیزیک‌دانان، «چن نینگ یانگ» و «رابرت میلز»، معارفه کردند تا چارچوبی برای توصیف نیروهای بنیادی از طریق ساختارهای هندسی اراعه دهد. در دنیای ذرات بنیادی، نظریه یانگ-میلز همان نقشی را ایفا می‌کند که قوانین نیوتن برای دنیای ماکروسکوپی دارند! این نظریه کوانتومی در واقع تعمیم نظریه الکترومغناطیس ماکسول است و اکنون پایه و مبنا زیاد تر نظریه ذرات بنیادی محسوب می‌شود.

یکی از مسائل مهم در نظریه یانگ-میلز، «شکاف جرمی» (mass gap) است. در این نظریه گفتن می‌شود که میدان‌های الکترومغناطیسی که با شدت نور حرکت می‌کنند، حامل بار می باشند و با ذرات کوانتومی به نام «گلوئون» توصیف خواهد شد. مطابق این نظریه، اگرچه این امواج با شدت نور حرکت می‌کنند، ذرات آن جرم مثبت دارند. فکر می‌شود همین ویژگی جهت شده نیروی قوی فقط در فواصل مختصر، درون هسته‌های اتمی،‌ مؤثر باشد.

شکاف جرمی از طریق آزمایش کشف شده و همانند‌سازی‌های کامپیوتری آن را قبول کرده است اما تا این مدت اثبات ریاضی دقیق و جامعی برای آن وجود ندارد. اثبات شکاف جرمی می‌تواند به فهمیدن بهتر ما از نحوه کارکرد نیروهای بنیادی و ساختار جهان زیراتمی پشتیبانی کند.

بر پایه قوانین جایزه هزاره، فردی که بتواند هریک از این ۶ قضیه دشوار را حل کند، باید راه‌حل خود را به CMI اراعه دهد. سپس هیئت مشورتی علمی (SAB) اثبات قضیه را تحت چند شرط بازدید می‌کند. اول این که اثبات باید کامل باشد؛ دوم این که باید در نشریه ریاضی معتبر قضاوت شود و تا ۲ سال سپس، جامعه ریاضی آن را بپذیرد. اگر این شرایط برآورده شود، SAB کمیته مشورتی متشکل از حداقل ۲ ریاضی‌دان برجسته و حداقل یک عضو از SAB برای بازدید دقیق اثبات تعیین خواهد کرد.

جمع‌بندی

مسائل جایزه هزاره مجموعه‌ای از ۷ قضیه‌ پیچیده و بنیادین ریاضیات است که سال ۲۰۰۰ مؤسسه ریاضی کلی به‌گفتن چالش‌هایی برای قرن بیست‌ویکم معارفه کرد و برای حل هرکدام جایزه‌ای یک‌میلیون دلاری تعیین شده‌ است. حل این مسائل عمق بیشتری به دانش ریاضی پایه‌ای بشر می‌بخشد و می‌تواند مسیرهای جدیدی در علوم گوناگون باز کند.

این مسائل شامل گمان ریمان، فرضیه یانگ-میلز، گمان هاج، قضیه P و NP، گمان برچ و سوینرتون-دایر و ۲ قضیه پیچیده دیگر می باشند که هرکدام با جنبه‌های خاصی از ریاضیات و علوم ربط دارند. هرکدام از این مسائل تا بحال یا بدون راه‌حل مانده‌اند یا فقط در موارد خاص حل شده‌اند.

فقط قضیه گمان پوانکاره کامل حل شده و ریاضی‌دان روسی، گریگوری پرلمان، راه‌حل آن را اراعه داده است. مسائل جایزه هزاره نشان‌دهنده مرزهای جاری علم ریاضی می باشند و حل آنها می‌تواند تبدیل دستاوردهای علمی قابل‌توجهی شود که نه‌فقط در ریاضیات، بلکه در حوزه‌های گوناگون نظیر فیزیک، نظریه اعداد و علوم کامپیوتر اثرگذار خواهد می بود.

سؤالات متداول